Monday, December 31, 2012
Naughty or Nice
Labels:
algorithm,
bell-curve,
normal,
random variable
Monday, December 24, 2012
Big Ho
So what is the Big Ho, the null hypothesis, regarding Santa Claus? A null hypothesis specifies the null position, one of no effect, perhaps a generally accepted default position, the status quo, or an established explanation. It should be a statement that can be falsified. But if this null hypothesis is true and Santa Claus does not exist, how can evidence possibly be gathered to refute this? This would be an incredibly difficult task. To reject this null hypothesis we would need evidence that Santa Claus does exist. Perhaps such as this cartoon by Dave Coverly.
Or we could select one of the more legal standards and reject based a preponderance of evidence, as in movie Miracle on 34th Street with thousands of letters addressed and delivered to Santa.
An easier course would consider the null hypothesis: Santa Claus does exist, our default position. It is much easier to falsify. If we gather evidence to reject this null hypothesis, we could reject the claim that Santa Claus does exist by reasoning towards its contradiction. Of course, Santa's required duties would seem to be easily contradicted by the laws of physics (see also here).
But with this null hypothesis and its easier approach to falsifiability, if we don't collect the evidence, we accept the default state:
Santa Claus does exist.
You decide.
Happy Ho-lidays.
Or we could select one of the more legal standards and reject based a preponderance of evidence, as in movie Miracle on 34th Street with thousands of letters addressed and delivered to Santa.
An easier course would consider the null hypothesis: Santa Claus does exist, our default position. It is much easier to falsify. If we gather evidence to reject this null hypothesis, we could reject the claim that Santa Claus does exist by reasoning towards its contradiction. Of course, Santa's required duties would seem to be easily contradicted by the laws of physics (see also here).
But with this null hypothesis and its easier approach to falsifiability, if we don't collect the evidence, we accept the default state:
Santa Claus does exist.
You decide.
Happy Ho-lidays.
Monday, December 17, 2012
Galton's Bayesian Machine
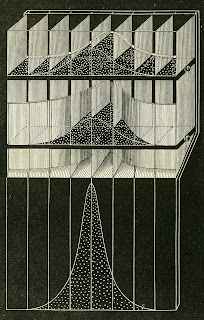
Chance magazine has an article by statistician and statistics historian Stephen Stigler on Galton's visualization of Bayes Theorem. He describes Galton's Bayesian machine, likely made up of beads, bins, and glass although the original device doesn't survive. These are, of course, familiar materials for Galton's statistical demonstrations.(This post was intended for some time ago. It got lost in the shuffle).
At the top level, beads are arrayed in deep vertical histogram bins representing the prior distribution, p(θ). A knob is turned and some fall into a bell-shaped horizontal room, representing the likelihood: f(x|θ). The room's back wall bulges away from us placing larger likelihood on central values of θ. If this room were moved more to the right, it would place larger likelihood on larger values of θ. At this second level, those beads falling to the front are retained, inside the bell curve wall, but some beads are rejected falling to the back, outside the wall. This performs the product: f(x|θ) p(θ). Of course at this level some bins are wide and deep, some are very shallow. The knob at this level is then turned and the beads are dropped to the bottom into vertical bins of equal width, rescaling them into a histogram proportional to the posterior distribution: f(θ|x)= f(x|θ) p(θ). Very clever and invented in 1877!
Monday, December 10, 2012
Not Normal Either and Why
I found this picture on Pinterest with the caption "Normal Distribution of cup lids." (Yes, I do troll for such things). I'm sorry, but yet again, this is not a normal distribution. Perhaps it resembles histogram bars from what could be a normal sample, piled high in the middle and lower on each side. But the problem is, as seen before, a normal distribution needs a measurement scale, a number line. Few small things on the left, few large things on the right, and many middle size things, of course, in the middle. This is the pattern shown by these lids, but there is no scale of measurement, no number line. It is not a frequency distribution of any obvious measurement. A similar stacking of items is shown below:
Scallop shells with different numbers of ribs (15 through 20) are stacked. This represents few small (scallops with 15 or 16 ribs), many middle-sized (with 17 or 18 ribs) and few large shells (with 19 or 20 ribs). This few-many-few pattern does resemble the cup lids above, but the lids have no measurement scale. The scallops are stacked into a real frequency distribution by their number of ribs. This is not a normal distribution since we are counting a discrete number of ribs. But it is a somewhat bell-shaped frequency distribution. The two scallops on the left have 15 and 20 ribs, respectively. More ribs seems to indicate an overall larger size or perhaps older scallop. A frequency distribution of a continuous measure of size, say mass or area, would be much more likely to be described a normal distribution.
Note: This is from the same book, Graphical Methods for Presenting Facts by Brinton (1914) that republished the earliest "living histogram" that I have found. This earliest one comes from Popular Science Monthly, September 1901 on page 447 of the article "The Statistical Study of Evolution" by C. B. Davenport.
Scallop shells with different numbers of ribs (15 through 20) are stacked. This represents few small (scallops with 15 or 16 ribs), many middle-sized (with 17 or 18 ribs) and few large shells (with 19 or 20 ribs). This few-many-few pattern does resemble the cup lids above, but the lids have no measurement scale. The scallops are stacked into a real frequency distribution by their number of ribs. This is not a normal distribution since we are counting a discrete number of ribs. But it is a somewhat bell-shaped frequency distribution. The two scallops on the left have 15 and 20 ribs, respectively. More ribs seems to indicate an overall larger size or perhaps older scallop. A frequency distribution of a continuous measure of size, say mass or area, would be much more likely to be described a normal distribution.
Note: This is from the same book, Graphical Methods for Presenting Facts by Brinton (1914) that republished the earliest "living histogram" that I have found. This earliest one comes from Popular Science Monthly, September 1901 on page 447 of the article "The Statistical Study of Evolution" by C. B. Davenport.
Sunday, December 2, 2012
This is Not a Normal Distribution
This is a display in the Anthropologie store in Georgetown, DC earlier this year. Ceramic cups are suspended from a shelf by ribbons. The length of the ribbons are generally arranged to produce a bell-shaped curve: shorter ribbons on each end and generally longer ones in the middle. But, no, this is not a normal distribution. The cups are not arranged or ordered by size, volume, weight, or price etc. There is no number line to represent some measurement. The is no frequency distribution showing few small, many average, and few large aspects of the cups. There are different size ribbons, but these do not represent a frequency count of how many instances of some aspect of a cup are accounted for. It does make a nice curving display suggestive only of a bell-shaped curve, but it is not even a rough representation of a normal distribution.
Labels:
bell-shaped,
distribution,
frequency,
histogram,
normal
Subscribe to:
Posts (Atom)







