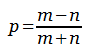Today is Memorial Day, a day to remember those that have fallen during US military service. It is also the traditional beginning of Summer. But Spring has been hard pressed to give-way to Summer here in Washington. Just two days ago. the temperature struggled upward, but stayed in the 60's (F), [10-15 Celsius]. A cold front kept it cold and rainy all day, much like much of our Spring this year.
Washington's iconic sign of Spring, the cherry blossoms, have long faded and fallen. This picture of fallen blossoms was taken a few weeks ago beneath a cherry tree that stretches like an umbrella above my front walk. What the picture shows is a realization of a spatial Poisson process. Such a random process counts, in continuous time, the number of petals that fall into non-overlapping regions. As the petals randomly land, the number of petals landing in any two separate paving stones are independent of each other. This would indicate that one petal, or its method or path falling from the tree, does not affect any other. The probability distribution of the count of petals on any paving stone depends only on the area of the stone.
I counted (likely with some error) the number of petals on each whole paving stone shown in this image. The mean number of petals on the square stones is 5.58. The mean number of petals on the rectangular stones is 8.71. If these were a result of a Poisson process these means should be proportional to the areas of the stones. The
rectangular, larger stones are half again larger than the square ones, that is, the ratio of the areas (rectangular/square) is 1.5. Under a Poisson process we should expect the same for the mean. And sure enough the ratio of the means is 8.71/5.58 = 1.56.
Monday, May 27, 2013
Monday, May 20, 2013
YADDA lunch-time
Only just recently have I taken notice of the wear pattern on the doors. This is the handle of the right hand door of two. It has the most wear, being opened primarily with right hands. Most wear is at a comfortable height to grab. Less wear can be seen higher as the top of the door handle ends. But there is also less wear lower on the handle as fewer hands grab the handle at a less comfortable height. Lower still there is little or no wear. There it is difficult and awkward to open the door with such a low grab. Top to bottom down the door handle we see less wear, more wear, and then less wear. What accumulates is a bell-shaped pattern of use and wear.
Labels:
bell-shaped,
distribution,
frequency,
YADDA
Monday, May 13, 2013
Airport Gumshoe
Another (disgusting) scatterplot of discarded chewing gum. This one around an airport parking lot trash bin. Although chewers have attempted to discard their gum in the bin, they have missed in many ways. Their deposits have missed to the left, to the right, they have fallen short of the bin, and perhaps even overshot it, although we can't see that in this image. The residues form a partially circular pattern of random scatter centered around the targeted trash bin. We've seen similar discards before, and the circular random pattern is common of normally distributed results that aim for a target and independently miss left or right or above or below the target.
Monday, May 6, 2013
Ballot Box Probability
A fun, geometric probability problem from Futility Closet that attributes it to W. A. Whitworth, but it is known as Bertrand's ballot problem after J. Bertrand who 'discovered' it eight years later. Yet another example of Stigler's law of eponymy: "No scientific discovery is named after its original discoverer," which, of course, was discovered by another: Robert K. Merton. The problem as explained by Futility Closet:
In 1878 W. A. Whitworth imagined an election between two candidates. A receives m votes, B receives n votes, and A wins (m>n). If the ballots are cast one at a time, what is the probability that A will lead throughout the voting?
The answer, it turns out, is given by the pleasingly simple formula
Howard Grossman offered the proof above in 1946. We start at O, where no votes have been cast. Each vote for A moves us one point east and each vote for B moves us one point north until we arrive at E, the final count, (m, n). If A is to lead throughout the contest, then our path must steer consistently east of the diagonal line OD, which represents a tie score. Any path that starts by going north, through (0,1), must cut OD on its way to E.
If any path does touch OD, let it be at C. The group of such paths can be paired off as p and q, reflections of each other in the line OD that meet at C and continue on a common track to E. This means that the total number of paths that touch OD is twice the number of paths p that start their journey to E by going north. Now, the first segment of any path might be up to m units east or up to n units north, so the proportion of paths that start by going north is n/(m + n), and twice this number is 2n/(m + n). The complementary probability — the probability of a path not touching OD — is (m – n)/(m + n).
(It’s interesting to consider what this means. If m = 2n then p = 1/3 — even if A receives twice as many votes as B, it’s still twice as likely that B ties him at some point as that A leads throughout.)The technical tool of pairing of reflections is an important technique for computing first return probabilities in the theory of random walks. It is sometimes known as André's Reflection Principle but as shown in this 2008 paper by Marc Renault, although Andre did solve the ballot problem, he used no geometric arguments. This reflection technique can be used to derive the distribution of the Kolmogorov-Smirnov goodness of fit statistic for the difference between two cumulative empirical distribution functions.
Subscribe to:
Posts (Atom)