Monday, June 30, 2014
YADDA Garage Gate
Yet Another Door Distribution Again (YADDA), this one on a gate in a garage stairwell showing a skewed distribution of hand placement opening the door. We've seen and described such patterns often, (YADDA in our list of labels). Since opening a hinged door is easiest with a long lever arm, more wear is shown near this gate's right-hand edge with less towards the door's pivot, resulting in this skewed pattern of wear.
Monday, June 23, 2014
Tornado Marginals
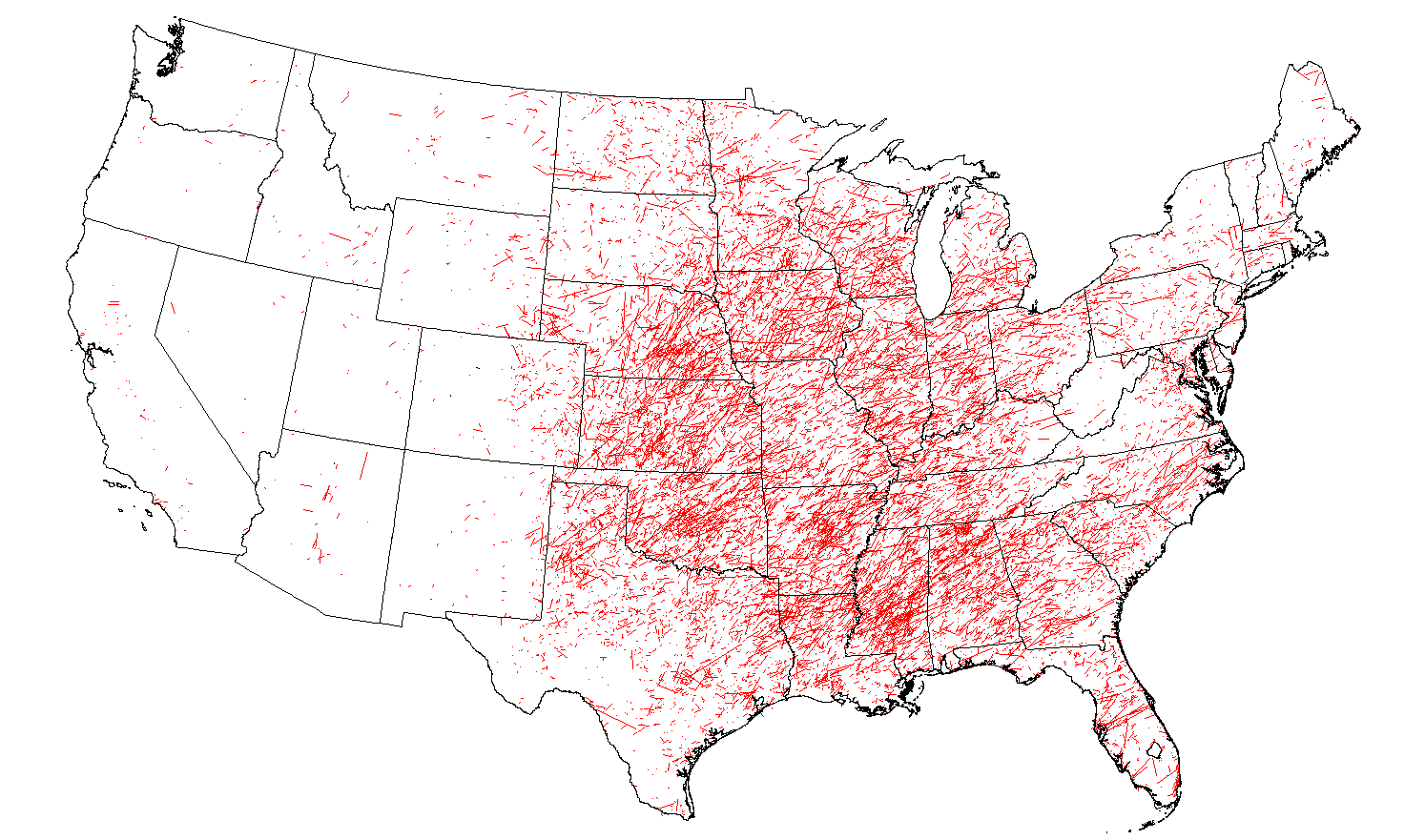
Inspired by this map of Waffle House restaurants by latitude and similar to global land mass marginal plots we've seen here before and corresponding world population plots, Tim Brice at the National Weather Service (NWS) in Texas produced maps showing the marginal distributions of tornado touchdowns by longitude and latitude.
Here's the joint distribution, a map of tornado tracks from 1950-2013 from the NWS
Here's the joint distribution, a map of tornado tracks from 1950-2013 from the NWS
(Thanks JCT).
.Monday, June 16, 2014
The Knotted String
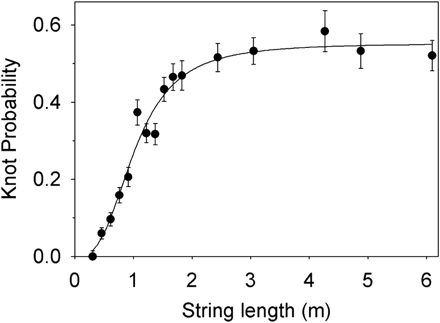
We've seen a paper on the Thrown String. Here is one on the Knotted String.University of California at San Diego physicists Raymer and Smith place various lengths of string in a box and film it tumbling for ten seconds. More specifically from their PNAS paper "Spontaneous knotting of an agitated string,"
Most of the measurements were carried out with a string having a diameter of 3.2 mm, a density of 0.04 g/cm, and a flexural rigidity of 3.1 × 104 dynes·cm2, tumbling in a 0.30 × 0.30 × 0.30-m box rotated at one revolution per second for 10 sec.Results from 200 trials noted the proportion of knots formed for various lengths. These results are plotted above. The dependence of this knotted probability on other physical properties of the string are shown in their table below:
They conjecture that the string confinement and rotation promote braiding at the ends of the string, producing the knots. As one report noted Apple's iPhone earbuds are 139 cm (55 inches) long and thus right at the 50% tangle-rate-sweet-spot at the top of the curve. Shorter earbuds would be welcome.
Labels:
binomial,
probability,
stochastic process
Monday, June 9, 2014
Monday, June 2, 2014
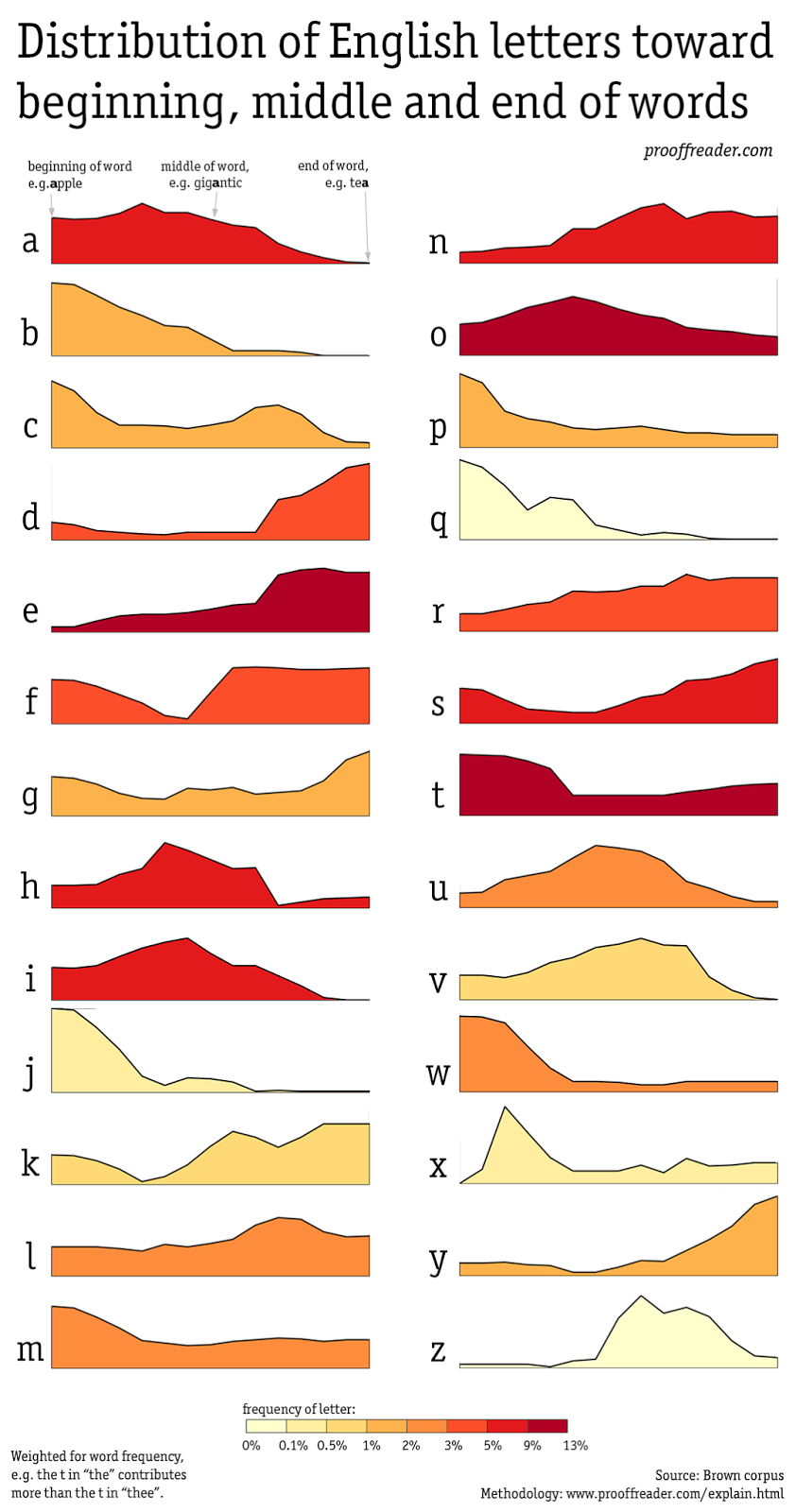
Ordinal Distribution of Letters in Words
We've previously seen the distribution of initial letters in English words. We've also seen the distribution of letter usage in the game of Scrabble. Here is a more complete distribution of letters developed by David Taylor on Prooffreader.com. His distributions are first color coded from pale yellow to deep red indicating the frequency of letter usage from least to most. Next he uses 15 ordinal bins of the relative positions of the letters that begin a word, through the middle of the word, and then the ending letters. Here is his example of how words of varying length were handled.
Normalizing the y-axis so that 100% represents each letter's greatest frequency is another approach. But he argues this makes interpretation difficult since the vertical scales really are not comparable.
And yet another approach is creating an integrated density so that each letter has a density curve with the same area. I think this works best, but he argues that for a letter like "z" with a narrower and taller central density compared to "a" with a broader and lower density, we give more weight to "z", viewing it as having more ink.
In the end he averaged these last two approaches, normalization and integration, to produce his curves. Check out more of his methods for these graphs at prooffreaderplus.
The 4-letter word "four" is apportioned here into only 5 bins. These bin percentages are accumulated across all the words in the Brown corpus via the Natural Language Toolkit. What remains is deciding what aspect of these accumulated percentages of ordinal data to plot to provide an informative display. If the raw percentages are used, comparisons are difficult between frequently used letters like "a" and rarely used ones like "z".
Logs were another possibility he considered, but these add their own interpretation problems.Normalizing the y-axis so that 100% represents each letter's greatest frequency is another approach. But he argues this makes interpretation difficult since the vertical scales really are not comparable.
And yet another approach is creating an integrated density so that each letter has a density curve with the same area. I think this works best, but he argues that for a letter like "z" with a narrower and taller central density compared to "a" with a broader and lower density, we give more weight to "z", viewing it as having more ink.
In the end he averaged these last two approaches, normalization and integration, to produce his curves. Check out more of his methods for these graphs at prooffreaderplus.
Subscribe to:
Posts (Atom)