Couldn't Resist

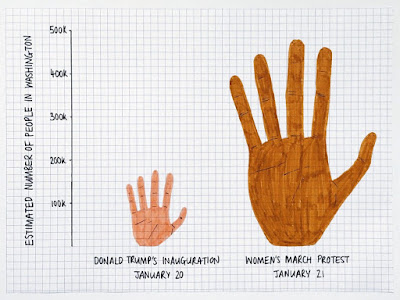
From Monica Calabi via Junk Charts via Wired. Of course, this is prone to the dimensional problem we've seen before.

Post Modern Bell Wear

Watch a fun video The Evolution of Tap Dance by Post Modern Jukebox with tap dancer Sarah Reich. Note the bell-shaped distribution pattern of wear on her tap platform: most wear in the middle and less towards the edges.

Self-Referential Santa

Futility Closet offers Raymond Smullyan's self-referential proof of the existence of Santa Claus:

A: Santa Claus exists, if I am not mistaken.
B: Well, of course Santa Claus exists if you are not mistaken!
A: So, I was right.
B: Yes.
A: So, I was not mistaken.
B: Yes.
A: Hence, Santa Claus exists.

Stepping Up

This is a ladder leading to an elevated playhouse for kids visiting Brookside Gardens in Maryland. The ladder reveals a frequency distribution of foot placement wear. On most steps we see more wear in the middle of the ladder rung and less wear towards the left and right edges. This leaves a bell-shaped pattern of use.

But a rung near the bottom has a bi-modal pattern, showing the wear resulting from both left and right feet. This doesn't persist on higher rungs. There the wear seems more central. So why not on the lower rung as well? Perhaps central steps on higher rungs feel safer. A care that is not that needed closer to the ground.

Guitar Fret Wear?

Here is an image from imgur of the fret board on a 1956 Fender Stratocaster guitar showing the frequency distribution of playing wear (thanks Scott). But many on Reddit disagree, calling it faked. Not being a guitar player, I can't judge. What do you think?

Fair, Minimal Symmetry Dice

Mathematician Henry Segerman demonstrates his 3D printed skewed or squished six-sided dice. He states "they work like ordinary dice". He exploits 3D symmetries to produce these isohedral dice with "just enough symmetry to be fair". Check out his video above and links to his extra footage.

Menu Basket Queue

This is a view of a basket of menus at a restaurant in Chincoteague, Virginia. Notice the pattern of marks left as groups of menus scratch the wall when they are returned to the basket. As customers are seated at the restaurant, they are given menus that are removed from the right hand side of the basket. After ordering, the menus are returned to the basket and placed to the right of the remaining menus. When a single is menu returned, it nicks the wall at a location that depends on how many menus are currently in the hands of customers. If few menus are out with the customers, more remain in the basket and the wall marks of this returning menu will be further to the right. If many menus are out with customers, say just before the lunch rush, this returning menu will make a mark on the wall further to the left.

But it is not often that a single menu is returned alone. It is much more likely that a group of menus will be returned to the basket in a bunch. The size of the bunch that is returned is random depending on the size of the party seated. Each of the menus in the bunch makes a mark on the wall as they are returned to the basket. What we see is a steady state distribution of the number of seated customers, with menus in hand, waiting for their order to be taken.