Monday, December 31, 2012
Naughty or Nice
Labels:
algorithm,
bell-curve,
normal,
random variable
Monday, December 24, 2012
Big Ho
So what is the Big Ho, the null hypothesis, regarding Santa Claus? A null hypothesis specifies the null position, one of no effect, perhaps a generally accepted default position, the status quo, or an established explanation. It should be a statement that can be falsified. But if this null hypothesis is true and Santa Claus does not exist, how can evidence possibly be gathered to refute this? This would be an incredibly difficult task. To reject this null hypothesis we would need evidence that Santa Claus does exist. Perhaps such as this cartoon by Dave Coverly.
Or we could select one of the more legal standards and reject based a preponderance of evidence, as in movie Miracle on 34th Street with thousands of letters addressed and delivered to Santa.
An easier course would consider the null hypothesis: Santa Claus does exist, our default position. It is much easier to falsify. If we gather evidence to reject this null hypothesis, we could reject the claim that Santa Claus does exist by reasoning towards its contradiction. Of course, Santa's required duties would seem to be easily contradicted by the laws of physics (see also here).
But with this null hypothesis and its easier approach to falsifiability, if we don't collect the evidence, we accept the default state:
Santa Claus does exist.
You decide.
Happy Ho-lidays.
Or we could select one of the more legal standards and reject based a preponderance of evidence, as in movie Miracle on 34th Street with thousands of letters addressed and delivered to Santa.
An easier course would consider the null hypothesis: Santa Claus does exist, our default position. It is much easier to falsify. If we gather evidence to reject this null hypothesis, we could reject the claim that Santa Claus does exist by reasoning towards its contradiction. Of course, Santa's required duties would seem to be easily contradicted by the laws of physics (see also here).
But with this null hypothesis and its easier approach to falsifiability, if we don't collect the evidence, we accept the default state:
Santa Claus does exist.
You decide.
Happy Ho-lidays.
Monday, December 17, 2012
Galton's Bayesian Machine
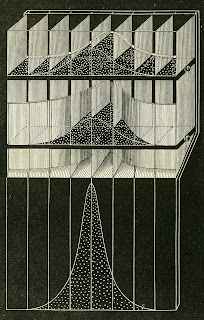
Chance magazine has an article by statistician and statistics historian Stephen Stigler on Galton's visualization of Bayes Theorem. He describes Galton's Bayesian machine, likely made up of beads, bins, and glass although the original device doesn't survive. These are, of course, familiar materials for Galton's statistical demonstrations.(This post was intended for some time ago. It got lost in the shuffle).
At the top level, beads are arrayed in deep vertical histogram bins representing the prior distribution, p(θ). A knob is turned and some fall into a bell-shaped horizontal room, representing the likelihood: f(x|θ). The room's back wall bulges away from us placing larger likelihood on central values of θ. If this room were moved more to the right, it would place larger likelihood on larger values of θ. At this second level, those beads falling to the front are retained, inside the bell curve wall, but some beads are rejected falling to the back, outside the wall. This performs the product: f(x|θ) p(θ). Of course at this level some bins are wide and deep, some are very shallow. The knob at this level is then turned and the beads are dropped to the bottom into vertical bins of equal width, rescaling them into a histogram proportional to the posterior distribution: f(θ|x)= f(x|θ) p(θ). Very clever and invented in 1877!
Monday, December 10, 2012
Not Normal Either and Why
I found this picture on Pinterest with the caption "Normal Distribution of cup lids." (Yes, I do troll for such things). I'm sorry, but yet again, this is not a normal distribution. Perhaps it resembles histogram bars from what could be a normal sample, piled high in the middle and lower on each side. But the problem is, as seen before, a normal distribution needs a measurement scale, a number line. Few small things on the left, few large things on the right, and many middle size things, of course, in the middle. This is the pattern shown by these lids, but there is no scale of measurement, no number line. It is not a frequency distribution of any obvious measurement. A similar stacking of items is shown below:
Scallop shells with different numbers of ribs (15 through 20) are stacked. This represents few small (scallops with 15 or 16 ribs), many middle-sized (with 17 or 18 ribs) and few large shells (with 19 or 20 ribs). This few-many-few pattern does resemble the cup lids above, but the lids have no measurement scale. The scallops are stacked into a real frequency distribution by their number of ribs. This is not a normal distribution since we are counting a discrete number of ribs. But it is a somewhat bell-shaped frequency distribution. The two scallops on the left have 15 and 20 ribs, respectively. More ribs seems to indicate an overall larger size or perhaps older scallop. A frequency distribution of a continuous measure of size, say mass or area, would be much more likely to be described a normal distribution.
Note: This is from the same book, Graphical Methods for Presenting Facts by Brinton (1914) that republished the earliest "living histogram" that I have found. This earliest one comes from Popular Science Monthly, September 1901 on page 447 of the article "The Statistical Study of Evolution" by C. B. Davenport.
Scallop shells with different numbers of ribs (15 through 20) are stacked. This represents few small (scallops with 15 or 16 ribs), many middle-sized (with 17 or 18 ribs) and few large shells (with 19 or 20 ribs). This few-many-few pattern does resemble the cup lids above, but the lids have no measurement scale. The scallops are stacked into a real frequency distribution by their number of ribs. This is not a normal distribution since we are counting a discrete number of ribs. But it is a somewhat bell-shaped frequency distribution. The two scallops on the left have 15 and 20 ribs, respectively. More ribs seems to indicate an overall larger size or perhaps older scallop. A frequency distribution of a continuous measure of size, say mass or area, would be much more likely to be described a normal distribution.
Note: This is from the same book, Graphical Methods for Presenting Facts by Brinton (1914) that republished the earliest "living histogram" that I have found. This earliest one comes from Popular Science Monthly, September 1901 on page 447 of the article "The Statistical Study of Evolution" by C. B. Davenport.
Sunday, December 2, 2012
This is Not a Normal Distribution
This is a display in the Anthropologie store in Georgetown, DC earlier this year. Ceramic cups are suspended from a shelf by ribbons. The length of the ribbons are generally arranged to produce a bell-shaped curve: shorter ribbons on each end and generally longer ones in the middle. But, no, this is not a normal distribution. The cups are not arranged or ordered by size, volume, weight, or price etc. There is no number line to represent some measurement. The is no frequency distribution showing few small, many average, and few large aspects of the cups. There are different size ribbons, but these do not represent a frequency count of how many instances of some aspect of a cup are accounted for. It does make a nice curving display suggestive only of a bell-shaped curve, but it is not even a rough representation of a normal distribution.
Labels:
bell-shaped,
distribution,
frequency,
histogram,
normal
Monday, November 26, 2012
What pie did you have on Thanksgiving?
What is your favorite pie? Did you have it for Thanksgiving? Here is a pie chart based on a National Public Radio report of a survey of America's favorite pies. The ultimate pie chart is, of course, here.
Monday, November 19, 2012
I'm taller than you
These are doors at the Rockville, Maryland location of the restaurant Matchbox. They are facing restroom doors near the bar. The one on the left of this picture is the door to the women's room. The one on the right is door to the men's room. Notice the scatterplot wear pattern of hand placement on each door. Men, generally taller, have worn away the paint on the door higher than that worn by the, generally shorter, women. Accurate measurements of the heights of the center of each wear pattern would give us estimates of height of hand placement on the door, likely to be about shoulder height as customers push on the door. Of course, being restrooms accurate measurements would just be weird! As it is, standing their with a camera was weird enough!
Similar door scatterplots can be found here and even another restroom door here.
Similar door scatterplots can be found here and even another restroom door here.
Labels:
distribution,
frequency,
scatterplot,
sex
Monday, November 12, 2012
Wind Vector Field
A dynamic sculpture called Windswept by artist Charles Sowers showing the vector field of wind direction on the side of the Randall Museum in San Francisco. The description from the artist's website says:
Windswept consists of 612 freely rotating wind direction indicators mounted parallel to the wall creating an architectural scale instrument for observing the complex interaction between wind and the building. Wind gusts, rippling and swirling through the sculpture, visually reveal the complex and ever-changing ways the wind interacts with the building and the environment.The measurements of such a vector field (including magnitude and direction) can be modeled and analyzed using directional statistics, like the wind swept pine needles of last week.
Monday, November 5, 2012
Pine Needles in a Circle
A view of the cover of a 'sanitary sewer,' (and why would you want any other kind?!). And as promised last week, notice the accumulation of pine needles around the edge of the cover. On this day the wind was quite gusty, blowing along this sidewalk from the bottom of the image to the top. Due to this wind direction, many more pine needles have accumulated and piled up around the cover at the bottom than at the top. This forms a histogram of the frequency distribution of wind action distributed around the circumference of the sewer cover.
If we had data situated around the circumference of a circle we could display it as a circular dot plot as shown below from the book "Circular Statistics" by Fisher. These are arrival times, on a 24hr clock, are for 254 patients at an intensive care unit. Few arrive in the morning, many more arrive in late afternoon and early evening.
An estimate of the density of circular sample can be computed using something like the code for a circular density curve in the programming language R, as shown below.
Such graphical tools are the beginnings of modeling on spheres and other manifolds studied under the general heading of directional statistics.
A probability density function defined on the real line is sometimes wrapped around a circle. We have earlier seen that the results of such wrapping give rise to the characteristic function, a fundamental tool of probability modeling.
Monday, October 29, 2012
Pine Needle Tracks
Guest Post by Dan Drake of the University of Puget Sound:
The attached picture is of the entrance to the library at the University
of Puget Sound. It's autumn here in Tacoma and there are lots of fallen
pine needles outside which the students track in. The door opens on the
right (on the left, to entering students) and you can see the
distribution is shifted that way near the door. The pine needles are
concentrated in the middle but show a few outliers, and the light color
in the middle shows dust and dirt brought in -- so there's a discrete
and continuous distribution.
The two dimensions of the carpet show a sort of time series: near the
door, people (and hence the dirt and pine needles) are shifted towards
the side of the door that opens, and as they walk into the library, they
tend to move to the center of the entryway.
Thanks for maintaining the blog -- I (and hopefully my students...)
enjoy it!
Thank you Dan for your interest and submission.
I'll have more on pine needles next week.
Monday, October 22, 2012
Queue Server Distribution
These are the feet of tourists at the Charleston, South Carolina visitor's center. The tourists queue up to get information about tours around the city and its attractions. There are only three servers helping them book their tours. These are the feet of the tourists being served. Others, waiting to be served, are standing to the left of the brass pole.
If no servers were busy, an approaching tourist would be served at the first position nearest the pole. This is on the right of this picture, where four people in one party are discussing their vacation options. Further down the line, two people are talking to server number two, and further still (at the top left of this picture) a lone visitor is with server number three.
The first server position gets the most business and other servers are called in to fill positions two and three as the queue requires.
We can see the server frequency of use in the next picture. There is more floor scuffing and wear at position one, less at position two, and the smallest amount of wear at position three - a discrete frequency distribution of server use.
Labels:
discrete,
distribution,
frequency,
queue
Monday, October 15, 2012
Subtle Condiment Curve
Here is a subtle wear pattern.
This is a table at our favorite restaurant. The right-hand edge is against the windows. Look carefully at the tabletop along this edge. The luster of the glossy tabletop has been worn down to a mat finish along this window edge. There is less wear, leaving a mat finish, at the corners of the table, closest and farthest from the camera. There is much more wear, along the window edge, in the middle. The rest of the table has a shiny glossy luster. The next picture shows us why:
This is a table at our favorite restaurant. The right-hand edge is against the windows. Look carefully at the tabletop along this edge. The luster of the glossy tabletop has been worn down to a mat finish along this window edge. There is less wear, leaving a mat finish, at the corners of the table, closest and farthest from the camera. There is much more wear, along the window edge, in the middle. The rest of the table has a shiny glossy luster. The next picture shows us why:
The missing condiments appear!
Salt, pepper, cheese, and a container of sweeteners live most often near the middle of this window edge. After use, they are repeatedly returned to this central location along the window edge, leaving more wear (shown by the greater area of mat finish). Occasionally, they are slid to the corners of the table - perhaps to get them out of the way for plates of food or for cleaning the table for the next customers. This wears less off the glossy table top. Smaller regions of mat finish are left near the corners.
A subtle bell-shaped pattern of wear is left behind. More wear in the middle less along the corners.
Monday, October 8, 2012
Garage Dings
One-car garages can be very small. Here is the driver's side wall of one such garage (thanks Laura). It displays the dings from opening the driver's side door in the tight space. Of course, the car is not parked in the same spot every time. Sometimes it rests a little farther forward in the garage and the door hits the wall more to the right in this image. Sometimes the car is parked just inside of the garage and the door dings fall on the left of this image. Most often the car is parked more centrally in the garage, leaving a greater frequency of door dings in the middle of the wall. This is a common pattern on this blog: little wear on the left, much more in the middle, and then little wear on the right. This is the typical pattern of a bell-shaped, symmetric normal distribution, although any unimodal even roughly symmetric distribution could be described similarly.
Perhaps the wall needs a little tweak along these lines:
These are plots that highlight, with color, the highest density regions of a measurement, like the location of the door dings. The densities are estimated by the smooth curves. The measurements are shown by their random arrangement of tickmarks on the horizontal axes below the density curves - just like the garage door dings. These are the plots from Hyndman, R.J. (1996) "Computing and graphing highest density regions" American Statistician, 50, 120-126. These plots are one of many featured graphics in the R graph gallery.
Laura needs some blue, red, and green tape!
Monday, October 1, 2012
Banging on the Exit
Dollar stores value their shopping carts. So much so they corral them with vertical poles that prevent their being rolled out the exit. Of course, many shoppers attempt to exit with the carts. The poles hit the top of the exit marking, scraping, and gouging the wall above the exit door. More wear near the center of the exit, less as the shoppers realize they can't leave with the cart and shove their eventual empty cart down the wall further marking its travels. A bell-shaped pattern of wear is left.
Monday, September 24, 2012
YADDA Sears - Yet Another Door Distribution Again
Bell-shaped wear pattern on the exit door at a Sears store. Lots of wear in the middle, less on the right-hand edge. The distribution appears skewed to the right. Would we see more of a left-hand tail if the handle was bigger or does the door open better by pushing on it more to the left than to the right?
See another door distribution in our video here.
See another door distribution in our video here.
Labels:
bell-shaped,
distribution,
frequency,
skew,
video,
YADDA
Monday, September 17, 2012
Discrete Text Wear
Texting has its own unique spelling and distribution of letter usage. I have been unable to find any published distribution of letter frequencies for texting. Are there any? If they were the same as standard English, the letter sets would have the following frequencies of use:
- abc 12.439
- def 19.243
- ghi 15.089
- jkl 4.925
- mno 16.773
- pqrs 14.347
- tuv 12.851
- wxyz 4.66
Monday, September 10, 2012
Counter Top Wear
See bivariate wear on a counter top here.
Monday, September 3, 2012
Soda Knees
Wear pattern of the knees of patrons who sat at the soda fountain counter of Clinton's Soda Fountain in Independence, Missouri. The wear pattern seems to be lower on the left. Is this from taller or shorter customers? Taller ones might sit farther from the counter and their knees may hit the counter lower. Why just on this one side? Chance or design?
Monday, August 27, 2012
Physics as a Continent
Here is a post from the blog Strange Maps showing Bernard H. Porter’s 1939 depiction of the history of physics as a continental map, complete with rivers of thought, villages named after the pioneers of physics, and a scattering of symbols. Several thinkers prominent to probability and statistics can be found on the map, being natural philosophers of their time. Included are Pascal, Laplace, the Bernoullis, and Galton, although his dates are wrong. He was born in 1822 but he died in 1911 not 1899 as listed. We need a map like this for just the field of statistics. It also brings to mind the old IBM timeline of the history of mathematics which has been updated by IBM for the iPad. From Strange Maps at Think Big via The Quantum Pontiff.
Monday, August 20, 2012
Venn Diagrams have gone to ELEVEN
Researchers Khalegh Mamakani and Frank Ruskey from the Department of Computer Science at University of Victoria, Canada have found the first "simple" Venn diagram of eleven sets. More here from the New Scientist.
"To such a deep delight 't would win me" to see such a diagram adapted to illustrate multiple regression! More here.
Monday, August 13, 2012
Tuesday, August 7, 2012
Law of Large Crowds (Monty Pythony)
A NOVA video about the Wisdom of Crowds. In his paper "Vox Populi" published in Nature, March 7, 1907, Sir Francis Galton investigated this wisdom at a Fat Stock and Poultry Exhibition writing:
Galton received the 787 cards with the estimates and, then he tabulated results. The actual "dressed" weight of the ox was 1198 lbs. The median of the crowd's guesses was 1207 lbs., so the crowd was off by only 9 pounds out of 1198 or less than 0.8%. This was better than any individual guess, even from the experts. Galton also found the upper quartile (q3) of the guesses to be 1236 and the lower quartile (q1) to be 1162. Thus the inter-quartile range is 74. He modeled the data with a normal distribution and estimated its standard deviation as 1/2 of this inter-quartile range or 37, (he calls this the probable error, p.e.). We could be a bit more accurate by using 3/4 of the inter-quartile range. He notes the skewness of the distribution of guesses, with the lower portion best modeled with a normal distribution with a standard deviation of 45 and the upper portion best modeled with a standard deviation of 29. He graphs horizontally the cumulative distribution function of the fitted normal (solid line) along with the cumulative relative frequencies of the data (dotted line).In these democratic days, any investigation into the trustworthiness and peculiarities of popular judgments is of interest. The material about to be discussed refers to a small matter, but is much to the point. A weight-judging competition was carried on at the annual show of the West of England Fat Stock and Poultry Exhibition recently held at Plymouth. A fat ox having been selected, competitors bought stamped and numbered cards, for 6d. each, on which to inscribe their respective names, addresses, and estimates of what the ox would weigh after it had been slaughtered and "dressed." Those who guessed most successfully received prizes.
This result is, I think, more creditable to the trust-worthiness of a democratic judgment than might have been expected.
Monday, August 6, 2012
Climate Dice Back in the Day
There's been much on blogs about "Climate Dice" and how humans are perhaps loading them. See the article by Andrew Revkin (New York Times) and more recently by Paul Krugman (New York Times) discussing the findings by James Hansen et al. on public perceptions of climate change, these links via Andrew Gelman. Basically, the data show that hotter extremes are becoming more likely.
Investigating the variability in climate, with analogies to random tosses of dice, has a long history, and not always considered in the correct way. C. F. Marvin, former chief of the US Weather Bureau, can be seen using such random methods in this article from Popular Science 1932 page 46. Describing this methods a bit more, this newspaper article from 1931 begins with an especially lyrical view of his work :
He does complicate things by confusing a sample and a population. He marvels at the fact that the products of the results on four tossed dice produces a histogram of measurements that is sparse and skewed to the right, resembling a sample record of actual precipitation. Of course, this is a population of all the possible products and its sparseness will always be present. As he notes, there is no way to fill in between the products that can only be produced with four dice. This has no relation to the sampling variability and sparse histograms, of many shapes, that could result come from a skewed but continuous population of measurements. Of course, it was 1931!
Investigating the variability in climate, with analogies to random tosses of dice, has a long history, and not always considered in the correct way. C. F. Marvin, former chief of the US Weather Bureau, can be seen using such random methods in this article from Popular Science 1932 page 46. Describing this methods a bit more, this newspaper article from 1931 begins with an especially lyrical view of his work :
I think here one should read "random" for "fortuitous". The article's final question is the title of a paper by Marvin the appeared in December 1930 Monthly Weather Review (pdf). In that paper he uses such random methods to simulate graphs of precipitation and compares the results to actual records questioning "who could pick out the natural from the chance order"?Common dice, inventions of the ancients and purveyors of financial distress to unlucky moderns, have risen to a new dignity. After having been rolled in many places, ranging from the cobblestones of side streets to the green covered tables in palaces of chance, they are now being tossed with analytical earnestness by the hands of science.In this new field the "galloping dominoes" are being used as a means of increasing man's working knowledge of the weather and its pranks. The greenback and silver involved when glassy eyed gamblers seek to get something for nothing are supplanted by graphs and slide rules in this new environment, where scientists seek the answer to the high sounding question, "Are meteorological sequences fortuitous?"
He does complicate things by confusing a sample and a population. He marvels at the fact that the products of the results on four tossed dice produces a histogram of measurements that is sparse and skewed to the right, resembling a sample record of actual precipitation. Of course, this is a population of all the possible products and its sparseness will always be present. As he notes, there is no way to fill in between the products that can only be produced with four dice. This has no relation to the sampling variability and sparse histograms, of many shapes, that could result come from a skewed but continuous population of measurements. Of course, it was 1931!
Labels:
distribution,
frequency,
histogram,
population,
skew
Monday, July 30, 2012
Happy Tweets from a Jellyfish
Average Happiness
A clever "jellyfish plot" from researchers at the Center for Complex Systems at the University of Vermont showing indexed percentiles from a study of the Positivity of the English Language. Words are scored by 50 people on a happiness scale (1=unhappy, 5=neutral, 9=happy). These 50 scores are averaged to produce an average happiness measure for each word. This is done for the 5000 most frequently occurring words on Twitter. Each point represents a word plotted by its average happiness and its rank by frequency of use (1=most frequent, 5000=least frequent). Percentiles (here deciles) of average happiness are graphed in a sliding window of 500 ranked words.The plot shows that generally the distributions of happiness, in frequently used or not so frequently used words, are skewed towards happier words, generally matching the marginal distribution curve shown on top. This finding was consistent across words from the New York Times, Google Books, and Music Lyrics.
But note the spread in the deciles decreases as the word usage decreases, and their average happiness generally gets smaller for less frequently used words. More details and graphs can also be found here.
Labels:
decile,
distribution,
frequency,
percentile
Monday, July 23, 2012
Curve of the fruit length of Oenothera lamarckiana
From the blog Scientific Illustration and Eyeball Mansion showing curves emphasizing the size (length) distribution of the Evening-Primrose (Oenothera lamarckiana). Drawing by botanist and geneticist Hugo de Vries. The top view is a cumulative distribution function flipped by ninety degrees (called by NIST the percent point function). The bottom view shows a larger sketched bell-shaped curve that is just a multiple of the smaller.
Labels:
bell-shaped,
distribution,
distribution function
Monday, July 16, 2012
Wednesday, July 11, 2012
Here's the right idea
G. S. Springer, a geology professor at Ohio University, has a cartoon that emphasizes the fact that the normal curve describes the distribution of measurements on a number line. Small measurements are on the left and large measurements are on the right. Those in the middle at "the top of the bell curve" are just average. These two getting ready to sled are "at the top" because they are average and there are so many others that are also average. The real "top" of the normal distribution are those large measurements (and sleds) on the extreme right of the number line.
Labels:
bell-shaped,
distribution,
frequency,
normal
Monday, July 9, 2012
The Puzzle of You
The previous post offered a Puzzle that showed a t-shirt design that conveyed the wrong idea about a normal curve. The problem is the point meant to indicate "YOU". This point is placed to indicate that "YOU" are on the low end of a scale of measurements.
The problem is, the design places the point on the curve, rather than on the number line that underlies the curve. To see the difficulty, compare the previous t-shirt design with manipulated image above (this is not an available shirt). Placing the point on the curve suggests that it slides along the curve.
Imagine the impression conveyed when it reaches the peak of the curve, as illustrated here. No doubt, "YOU" would say you were at the top of the heap, even though your measurement would be very common, the most likely one that we could observe. This "top of the curve" error is common (no pun intended). The curve is not the distribution, the curve only describes the distribution. The labeled point should be on the supporting number line, not on the curve.
The problem is, the design places the point on the curve, rather than on the number line that underlies the curve. To see the difficulty, compare the previous t-shirt design with manipulated image above (this is not an available shirt). Placing the point on the curve suggests that it slides along the curve.
Imagine the impression conveyed when it reaches the peak of the curve, as illustrated here. No doubt, "YOU" would say you were at the top of the heap, even though your measurement would be very common, the most likely one that we could observe. This "top of the curve" error is common (no pun intended). The curve is not the distribution, the curve only describes the distribution. The labeled point should be on the supporting number line, not on the curve.
Monday, July 2, 2012
Puzzle: How does this t-shirt design get it wrong?
Here is a t-shirt design available from ThinkGeek. The point labeled "YOU ARE HERE" is placed to convey an incorrect idea about the normal distribution. What is wrong here? Answer in the next post.
Labels:
distribution,
frequency,
normal,
outlier
Wednesday, June 27, 2012
Brass Polishing Distribution
Monday, June 25, 2012
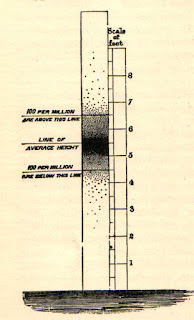
MOMA Height Exhibit
Here is a proper depiction of a height distribution. From the exhibit "Performance 4: Roman Ondák" that was at the Museum of Modern Art in 2009.
Of course, Sir Francis Galton had this idea over a century ago. See his book on Hereditary Genius on page 28.
Labels:
distribution,
frequency,
galton board,
normal
Friday, June 22, 2012
Curve (maybe), Distribution NO.
Found on Flickr with the caption "Standard Normal Distribution".
Perhaps it is suggestive of histogram bars often seen with a bell-shape of a normal distribution. But what variable is being measured? See "NO, NO, NO, the Wrong Idea" in the previous post here.
Perhaps it is suggestive of histogram bars often seen with a bell-shape of a normal distribution. But what variable is being measured? See "NO, NO, NO, the Wrong Idea" in the previous post here.
Tuesday, June 19, 2012
NO, NO, NO. The wrong idea.
 Found on Flickr here with the caption "normal distribution class photo".
Found on Flickr here with the caption "normal distribution class photo".A bell-shaped normal curve is not the normal distribution. The curve only describes the distribution. A normal distribution is a particular arrangement of measurements on a number line.
This photo seems to want to depict a normal distribution of the heights of students. If height is the variable of interest, the horizontal axis should be a number line with all the smallest students on the left and those taller would be placed further to the right. If the heights of the students had a bell-shaped histogram we would expect to see very few short students, very few tall students, and most of the students would have heights that fall between those extremes. This photo puts the tall students in the middle and shorter ones on the extremes. Maybe they have illustrated a bell-curve, but no number line is used, so no distribution (normal or otherwise) could be represented.
Labels:
bell-shaped,
distribution,
histogram,
normal
Subscribe to:
Posts (Atom)