Kernel Pinterest

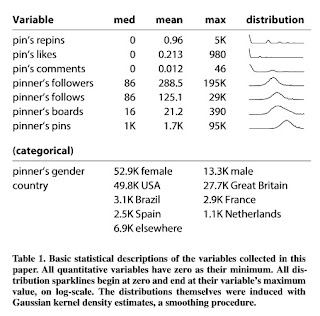
Here is a nice idea for displaying a bit more than summary statistics on the variables included in regression studies. This is from the paper "I Need to Try This!": A Statistical Overview of Pinterest. Pinterest is a pin-board photo sharing website. Among other things, this study models the number of re-pins of a given photo with a Negative-Binomial regression.

The table above shows the medians, means, and maxima for non-negative count data included in the regressions. The minima are all zero. Along with these summary statistics are small thumb-nail kernel density estimates of the distributions of the variables. Now granted the variables involved take on only integer values and these distribution curves are continuous, but it is much better than the usual limited summary statistics, shown below, that are often given in other regression studies.

Venn Disease

From the New York Times, dynamic Venn diagrams about diseases of the elderly.

A Venn diagram based on data from the study, by the National Center for Health Statistics in 2010, shows just how often these three conditions [high blood pressure, heart disease, and Alzheimer's disease] coincide in patients, and why this overlap is becoming an important new field of study.

Gumshoe

Tim Horton's Coffee and Bake Shop on W 34th Street near 7th Avenue sits at a transportation hub for New York City. Penn Station is a block away, out of town buses load and unload nearby, city buses and taxis, prevalent throughout the city, cluster here to serve the new arrivals. People also wait for the same trains, buses, and taxis. To enjoy their fresh coffee and donut during their wait they must discard their chewing gum. Unfortunately, for hygiene but fortunately for us, they drop it on the sidewalk. These sticky discards darken as they age, collecting dirt and grime and displaying a scatterplot of these messy leavings. Many wads have been dropped near the shop's window and fewer in less concentrated semi-circular arcs moving away from the window. The window seems to be the central point for some transportation queue. Here is left on the sidewalk another truncated view of a circular scatterplot of impatient deposits.

YADDA belly

Yet Another Door Distribution Again. This time we have the wear pattern on the inside of the doors at Potbelly's sandwich shop in Rockville, MD. This is the typical pattern of people holding the door open to enter the shop. Their fingers wrap around the edge of the door. As is usual, more hands seem to have left their entry mark by opening the right-hand door (the left-hand door in this inside image). The most wear is shown at a comfortable height, perhaps shoulder-high or a little lower. There is less wear higher-up and also lower-down where it gets more awkward to hold the door open. There does seem to be a longer lower tail on this bell-shaped pattern of wear suggesting kids have also left their marks.

Salty Residuals

Washington, this Winter, has not been wearing "on his smiling face a dream of Spring". On the contrary, Spring has been continually cold and damp much like the movie Groundhog Day. Just last week we had an unusual mid-March snowstorm. Groundskeepers spread salt along campus walkways to speed the snow melt. Their spreader sprayed the salt left and right as they drove down the path. After melt, the salt remained attracting moisture, absorbing - not reflecting - the light that fell on it, leaving a dark, wet residual on the asphalt.

At every point down the walk we can see the horizontal spread of the dark residuals, much concentrated near the center of the walk with lesser concentrations to the right and left. Horizontally, what remains is a bell-shaped distribution of salt deposition. The distribution has this same, consistent shape at each place down the walk. In this angled, perspective view the distributions look more skewed to the right. But the symmetry can be seen more accurately in the rotated image below.

This rotated image now shows the distributions in vertical slices as we move horizontally along the walk. The distributions are centered along the same horizontal line with the same shape and degree of vertical spread.

This is exactly the image of ideal residuals from a simple linear regression fit to data plotted against an explanatory variable from a uniform design. Of course, a different design placement of the explanatory variable would vary the pattern horizontally, but not so vertically. Other design patterns could arise from the spreader moving faster or slower down path leaving a more uneven, erratic deposition of salt - more at some steps along the walk than at others. But the assumptions for such a regression model still require identical, vertical normal distributions of scatter around a straight line of means irrespective of the horizontal position down the path. For an even, uniform walk down the path, our salty residuals model and reflect the ideal behavior of regression residuals.