Just Marginal Joints

Here is a joint distribution of wear on the counter top of a Home Depot. The counter top was originally white. This has worn away to reveal various layers of shading in the laminate and further into the underlying wood of the table. The innermost area has been actually gouged out by many tools, cans of paint, and other heavy hardware. We see nested triangular patterns of wear revealing the joint distribution of tool placement on the counter and their movement across the checkout scanner.

But wait. There's more, as they say on infomercials. Not only do we get the joint distribution of wear, we also get one marginal distribution of wear along the front edge of the counter. As customers drag their purchases onto or off of the counter they leave a bell-shaped pattern of use along that front edge.

Our Video

Award for Best Evidence of Inspiring Students at the 2011 Joint Statistical Meetings in Miami Beach. Double click on video for full screen.

YADDA: Yet Another Door Distribution Again

This is an edge-on view of an open door. Notice the wear pattern along the edge. Another bell-shaped frequency distribution of wear.

Mc-Bell-Shaped

Wear caused by hands (fingers?) holding a door? Perhaps left hand fingers in the PULL slot and thumbs wearing away on the door edge. More frequent wear near the middle and less above and below. We've seen this pattern before, like here. There will be more to come. This pattern is quite common. Find one for yourself and share.

Skyscraper Frequencies

A sculpture of a keyboard with the key's height proportional to its letter's frequency of use in English. Looks like a small city block full of skyscrapers. How would the block look different if the frequencies of use were in another language. Via Geekologie. Thanks to Laura.
I examined related frequency and language questions here.

Automated Histograms c. 1962

This is a device, from Nature in 1962, to construct a histogram during an experiment of stimulus-response times. The histogram forms by the careful timing of the release of ball-bearings into plastic bins. As a stimulus is given to a subject, the machine comes to life, starting a motor and engaging an electro-magnet. The motor hums, driving a treadmill-type belt at a constant rate. A ball-bearing is then projected onto the underside of the belt by a solenoid. The ball-bearing is held fixed at a point along the moving belt by the magnet. Once the subject responds to the stimulus, the electro-magnet is switched off, and the ball-bearing drops into the appropriate bin indicating the response time. The histogram grows as more response times are measured. It is suggested that the mean can then be found by balancing the display, and the variance by finding its moment of interia.

Earthquake/Population Density Map

A map of global earthquake intensity, showing magnitude and density of seismic activity weighted by population (larger version here). According to Views of the World this map allows us "to understand the earthquake intensity in relation to today’s population distribution, and thus gives an idea of where most people are of risk related to seismic activity." The algorithm uses kernel density estimation followed by a density equalizing algorithm.
Via The Map Room.

Friday Fun: Comparing Apples & Oranges

A totally fair, balanced, unbiased comparison. Really. No really! See more of this chart at: smarter.org via junkcharts.

March Madness: It Didn't Happen Again!

Since 1985, when the NCAA Division I Men's Basketball Tournament expanded to 64 teams, a team seeded (or ranked) 16 (last in each of the four regions) has never beaten a team seeded first. Over the 27 years from 1985 to 2011, (108 pairings) the number 1 seed has won by as much as 58 points (in 1998, Kansas(1) over Prairie View(16) 110-52). But twice over that time, both times in 1989, the number 1 seed narrowly edged out the number 16 seed by only 1 point (Georgetown(1) over Princeton(16) 50-49 and Oklahoma(1) over East Tennessee State(16) 72-71.

The histogram above shows the winning point margins. It closely fits a normal distribution with a mean of about 25 and a standard deviation of about 12. This gives us an estimate of the probability that a 16 seed could beat a number 1 seed, as just the probability that this normal distribution is less than zero. Here, we get a value of about 2%.

Wait 'til next year!

P.S. (3/20/2011)
A colleague observed that since a 16 seed has never won over a 1 seed in 108 trials of men's basketball (although it has happened in women's in 1998, 16 seed Harvard over 1 seed Stanford 71-67) that a 2% probability of an upset is perhaps too high and the probability should be less than 1% (1/108). But this treats a trial as only a success or failure and ignores how close the score was to an upset. A value near 1% is likely too small.

Multiple Regression Model c. 1911

A multiple regression model from George Undy Yule's "An Introduction to the Theory of Statistics" (1911) page 242. The residuals can be seen in the edge-on view.

Contours of Use

Here are scatterplot contours of hand placement in opening a door at a health center stairwell. The door itself is the darkest color shown, but it has been painted over with white, blue, and peach(?) colored paint. As thousands of hands push the door open they slowly rub away some of the paint, leaving bivariate contours of greatest use. Horizontal and vertical frequency of hand placement can be readily seen in the paint wear pattern.

3D Punching Bag Scatterplot

A 3D scatterplot made of 1300 punching bags (click picture for larger view) by artist Michael Kalish from Wired, with an impressive 2D marginal scatterplot of Muhammad Ali.

Matching Normal Densities

An image of the wear on exit doors at a Barnes and Noble bookstore in Rockville, Maryland. Most wear is located a little below shoulder height as customers push on the door with outstretched arms as they exit. Or are they holding open the door with fingers as they enter? It turns out it's both. (Yes, I stood there and watched!). It's both uncomfortable and inefficient to open the door much higher or much lower. We're left with a greater frequency of use centrally located with less and less wear above and below: a unimodal frequency distribution of wear. Considering that human height is approximately normally distributed, the patterns here should reflect that normality. It's interesting to note that the left hand door seems to have a frequency distribution of wear that sits slightly above that for the right hand door.
Any ideas as to why?

Musical Stacked Histograms

This graphic has gotten a lot of play in the past few weeks. It purports to show the collapse of the global music industry. The image is discussed on Junk Charts where attention is directed at the mystery of the decline in CD sales around 2001. An interesting image, but as Michael DeGusta of Business Insider shows not all is what it seems. He details the graphic's recent history and notes several problems: It's really only US sales figures and it's not adjusted for inflation, among other problems. He provides other images of music sales data and this correction of the chart in 2011 dollars:
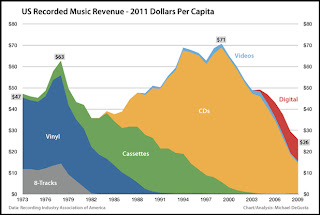
Here we see a problem with interpreting such an image. One commenter on Junk Charts notes:

"We might be able to tell if the Digital Sales area was not hidden behind the CD Sales area. Hence the problem with area charts."

To which another responds with the correct answer:

"Digital sales isn't hidden behind the CD sales - its stacked on top. I know it looks like a range of mountains, but it isn't. I think. That's the perceptual problem with charts stacked like this."

Yes, it is not one curve sitting behind another, like a range of mountains. The histogram information is stacked on top of the other curves. Stacked histograms are often used when displaying time dependent data, like for following. But not always.
Here is an image of a "living histogram" that organizes men and women of different heights into frequency classes. The men's histogram is easily seen. The women (dressed in white) are added or stacked onto the men's histogram classes. It does give an indication of the population heights for both, but it's more difficult to view the women's histogram alone. The same holds for the graphic of music sales. But I want to see the time axis extended further into the past, showing sales of 45s, 78s, and then even Edison wax cylinders!

"Mnemonic" is itself a (Poisson) mnemonic

See The Futility Closet. I can now use the Poisson distribution to help me remember how to spell "mnemonic"!

Bathroom Exits

This is a view of the inside exit door of the men's restroom at a movie theater in Germantown, Maryland. (I had to be careful with the camera in there!)

Notice the spatial pattern of wear on the main part of the door and the vertical wear pattern on its left-hand edge. This illustrates a bivariate frequency distribution of hand placement along with a marginal frequency distribution (on the left) of just the vertical hand placement.

Users of this restroom exit by pushing on the door and proceeding around to the right towards the theater. As the men do so, they don’t seem use the metal push panel provided. It doesn't seem to be designed properly for mens' heights. Instead, the men seem to push higher on the door wearing off the red paint. We see a two-dimensional spatial distribution of their hand placement. The wear pattern shows both the horizontal and vertical placement of their hands as they push the door to exit.

But the picture also shows more. As the men exit the door, they proceed out to the right, rubbing their hands on the edge of the door. The resulting wear pattern shows the marginal distribution of the vertical position of their hands. They push the center of the door and then scrape their hands on the edge producing both the two-dimensional spatial distribution followed by a one-dimensional marginal distribution.

I noticed the open exit door on the women's room. I couldn't get the picture there. But the women's door had much less wear on the door. They seemed to use the metal push plate to open the door. It was mounted more correctly for their height or perhaps the women were in less of a hurry.

BMI Over Time

Much like Gapminder highlighted in a previous post, the Washington Post has created a scatterplot of national body mass indices (BMI) overtime. Can you find a country whose national BMI decreased over a stretch of time contrary to almost every other country?
For an individual, body mass index is not the most valid index of how overweight you might be, despite the claims of the Centers for Disease Control. Keith Devlin points this out well in his column for the MAA.

NYTimes Investment Graphic

This NYTimes graphic makes me feel better about my very conservative investments.